Cuerpos Finitos
Los cuerpos finitos son un conjunto de números como su nombre lo indica, finitos, y que tienen una cardinalidad o número de elementos definido, que es la potencia de un número primo.
Matemáticamente se definen como: Fp = {0,1,2,…p-1}
Ejemplo de un cuerpo finito F5 = {0,1,2,3,4}
En los cuerpos finitos tenemos 2 operaciones, suma(+) y multiplicación (*). Para que un cuerpo finito exista se deben cumplir las siguientes relgas:
- deben ser cerrados, es decir si a y b estan an al conjunto a+b y a*b están en el conjunto.
- debe existir una identidad aditiva, es decir a+0=a
- debe existir la identidad multiplicativa, a*1=a
- debe existir el aditivo inverso, si a está en el conjunto -a debe estar en el conjunto
- debe existir un inverso multiplicativo, si a está en el grupo y no es 0, a-1 esta en el grupo, definido como el avalor que hace que a*a-1=0
cuerpos de enteros modulo p
El conjunto de enteros modulo p consiste en todos los enteros de 0 a p-1 en los que las operaciones funcionan bajo la aritmética modular. La aritmética modular es una herramienta que podemos usar para que nuestro cuerpo finito sea cerrado bajo para las operaciones de suma, resta, multiplicación y división. La operación módulo (denotada por el símbolo % o bien la palabra mod) consiste en obtener el residuo de una división de un un número entre otro. Por ejemplo:
7 % 3 = 1
1747 % 241 = 60
-13 % 12 = 11 (funciona inclusive para números negativos)
y para operaciones:
Suma, (18 + 9) % 23 = 4
Resta, (7 - 14) % 23 = 16
Multiplicación, (4 * 7) % 23 = 5
aditivo inverso, -5 % 23 = 18, 5 + (-5) = 5 + 18 % 23 = 0
inverso multiplicativo, 9-1 % 23 = 18, 9 * 9-1 = 9 * 18 % 23 = 1
Ahora ya tenemos todos los elementos para restringir nuestras curvas elipticas sobre un cuerpo finito Fp
Así se ve la curva de Bitcoin sobre un cuerpo finito de F24
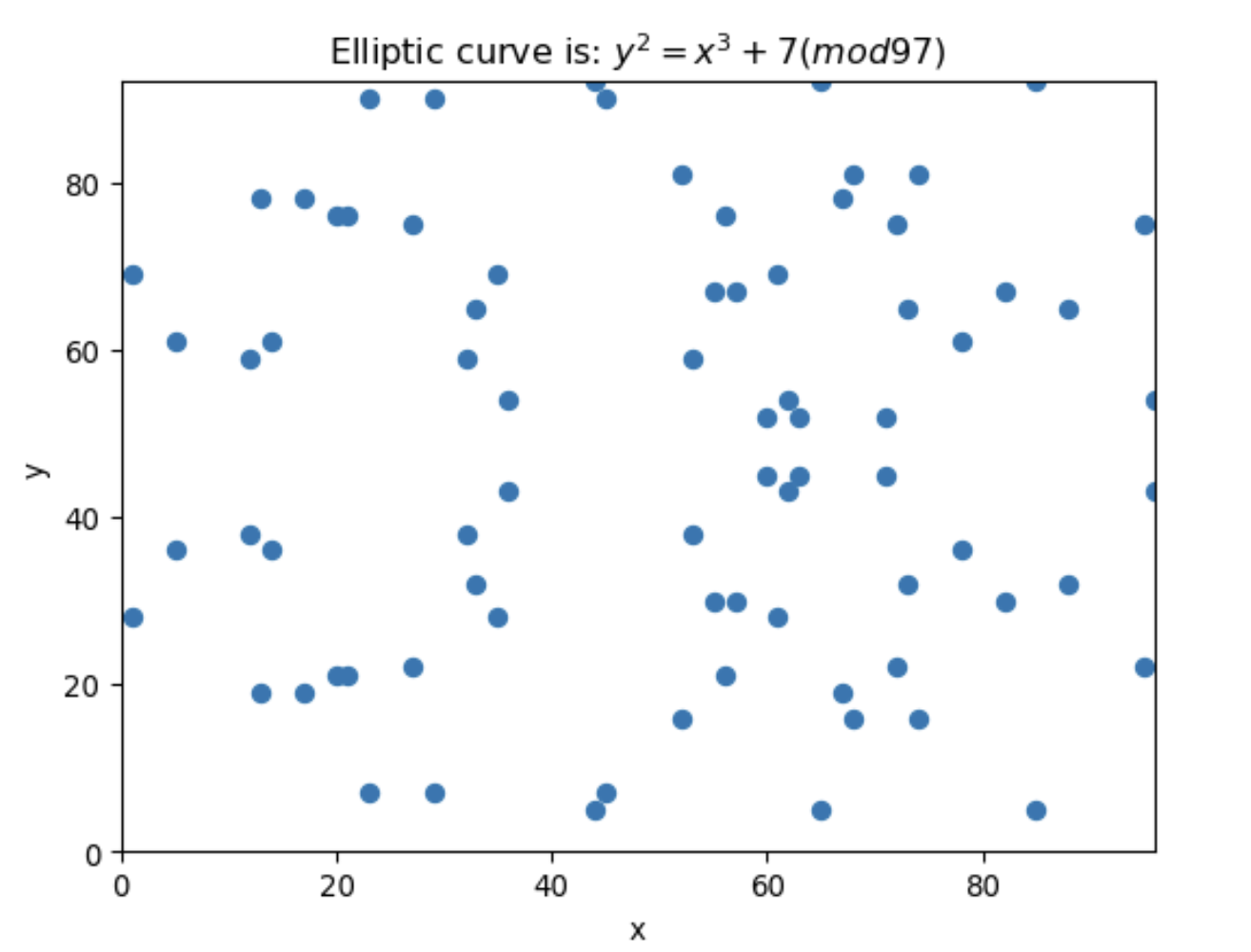
Curva Bitcoin campos finitos
De esta curva podemos notar 2 puntos fundamentales, 1) la curva se compone por una serie de puntos que no firman una curva como cuando graficabamos la curva sobre números reales y 2) es simétrica en el eje de las y
Lo que es interesante es que podemos seguir utilizando la aritmética que definimos para los cuerpos finitos (suma, resta, multiplicación, aditivo inverso e inverso multiplicativo).
Adición de puntos
Como ya notamos, los puntos son simétricos sobre una cierta línea, lo que significa que podemos seguir llevando a cabo la adición de puntos P+Q=-R, donde dibijamos una línea conectando a los puntos P, Q y R y reflejando R sobre el eje de las x obtenemos -R.
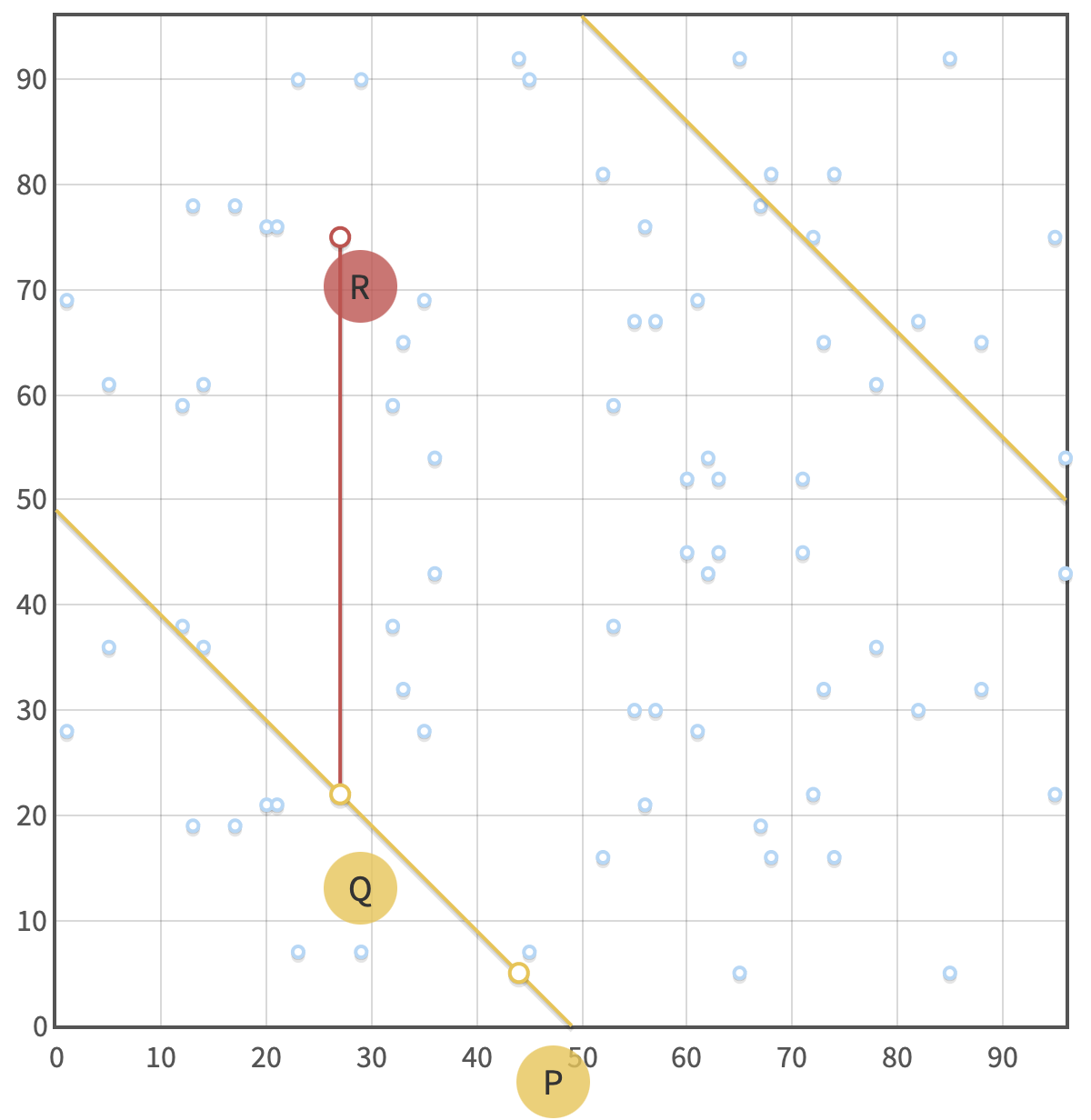
Curva Bitcoin adición campos finitos
Es importante notar que la línea que une a los puntos se ve de una forma completamente distinta sobre un cuerpo finito.
Suma algebráica
Las ecuaciones para la suma algebráica son exactamente iguales a las del post anterior, lo unico adicional es que llevan a cabo la operación módulo al final de cada expresión, es decir se aplica la operación módulo al resultado.
Si P y Q son distintos
\[x3 = s^2-x1-x2 \mod p\]
\[y3 = s(x1-x3)-y1 \mod p\]
Si P y Q son iguales
\[x3 = s2-2x1 \mod p\]
\[y3 = s(x1 - x3) - y1 \mod p\]
Multiplicación escalar
Debido a que podemos sumar un punto a si mismo, podemos intruducir nueva notación.
(10,15) + (10,15) = 2 * (10,15)
De forma similar como tenemos asociatividad, podemos añadir nuevamente el punto
2 * (10,15) + (10,15) = 3 * (10,15)
Y podemos hacer esto cuantas veces deseemos, A esto es a lo que llamamos multiplicación escalar, esto es porque tenemos un número frente al punto. Podemos hacer esto porque hemos definido la adición de puntos y es asociativa.
Llevar a cabo la multiplicación escalar es trivial, pero hacer lo opuesto,es decir la división, no lo es. A esto se le llama el problema del logarítmo discreto y es la base de la criptografía de curvas elípticas.
Otra propiedad de la multiplicación escalar es que en un cierto múltiplo, llegamos al punto al infinito o cero (0), (recordemos que el punto 0 es la identidad aditiva). si imaginamos un punto G y realizamos la multiplicación escalar hasta llegar al punto al infinito tenemos que:
{G, 2G, 3G, 4G, … nG} en donde nG = 0
A esto es a lo que se le llama un grupo, o mejor dicho un grupo de ciclo finito, lo que realmente queremos generar, para el propósito de la criptografía de llaves públicas, son los grupos de ciclo finito y sucede que si tomamos un punto de generación de una curva eliptíca sobre cuerpos finitos, podemos generar un grupo de ciclo finito.
Hasta aqui, en este post, hemos introducido los cuerpos finitos, la aritmética modular, las curvas elípticas sobre cuerpos finitos y lo mas importante la multiplicación escalar y los grupos de ciclo finito que son la base para la critografía de curvas elípticas y en particular para la que veremos en el próximo post Criptografía ECDSA.
