La seguridad de Bitcoin se basa en el manejo de llaves públicas y privadas. ECDSA (Elliptical Curve Digital Signing Algorithm por sus siglas en inglés) es la criptografía detrás de las llaves públicas y privadas en Bitcoin. Consiste en la combinación del manejo matemático de las curvas elípticas y los cuerpos finitos para crear ecuaciones que funcionan en un solo sentido, es decir que puedes escoger un número como tu llave privada y derivar, por medio de algoritmos, una llave pública. Sin embargo, la operación inversa que, a partir de una llave pública puedas obtener la llave privada, no es posible.
Curvas Elípticas
Una curva elíptica es la serie de puntos definidos por la siguiente ecuación:
\[y^2=x^3+ax+b \]
Esto excluye a las curvas que no cumplen con lo siguiente\[4a^3+27b^2=0 \]
En particular Bitcoin esta basado en la criptografía que utiliza la siguiente ecuación denominada secp256k1 :
\[y^2=x^3+7 \]
Esta ecuación es representada por la curva que a continuación se muestra:
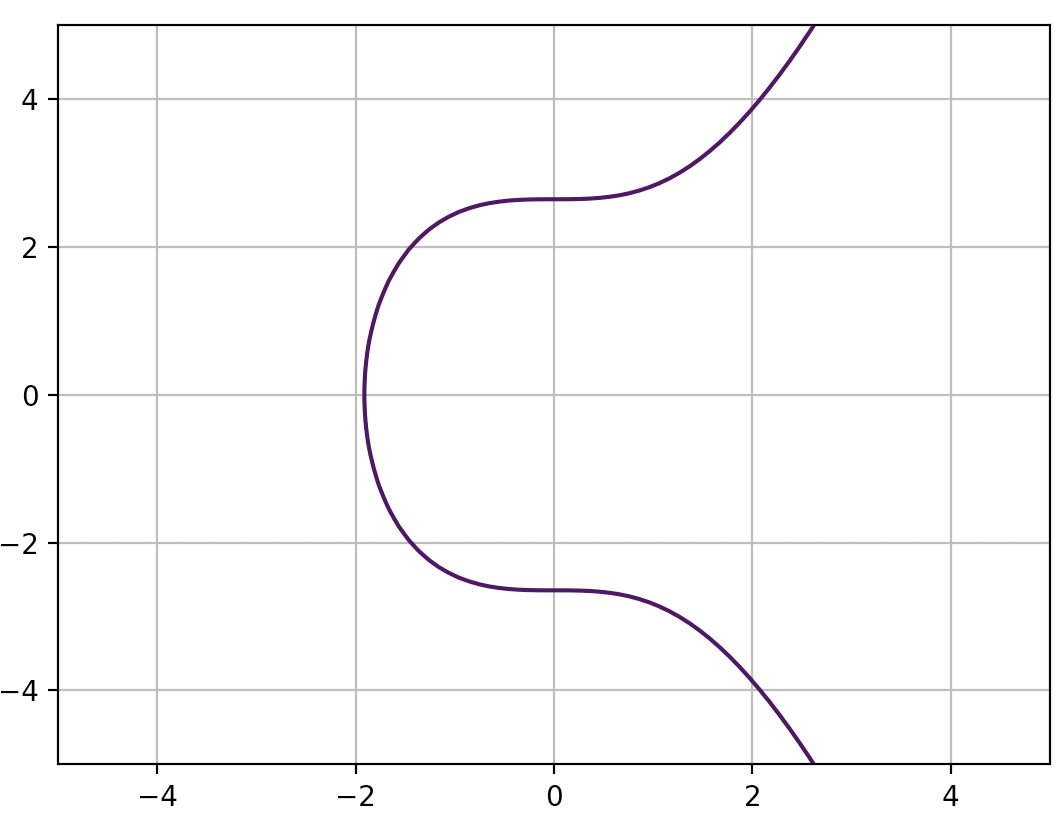
Curva elíptica Bitcoin
Como vimos, la ecuación original contiene los términos 4a
Podemos definir un grupo dentro de las curvas elípticas si:
- los elementos del grupo son puntos dentro de la curva elíptica
- el elemento de identidad es el punto al infinito 0
- el inverso de un punto P es uno simétrico sobre el eje de las x
- la adición es dada bajo la siguiente regla: dados tres puntos alineados, distintos a 0, P, Q y R, su suma es igual a P+Q+R=0
Las curvas elípticas son útiles por lo que se le denomina adición de puntos, cuando deseamos hacer una operación con dos puntos para obtener un tercer punto sobre la curva. A esta operación se le llama suma, porque comparte varias propiedades que asociamos con la operación de sumar. Por ejemplo, la conmutatividad, si sumamos al punto A con el punto B, es lo mismo que sumar el punto B al punto A.
Si para la suma de los puntos P=(x,y), Q=(x,y) realizamos la proyección de una recta que toca los primero dos puntos, obtendremos un tercer punto (x,y) en donde la curva es tocada por tercera vez, y si este punto lo reflejamos haciendo una inversión sobre el eje de las x, tendremos como resultado el punto -R(x, y) tal y como se muestra en la gráfica siguiente:
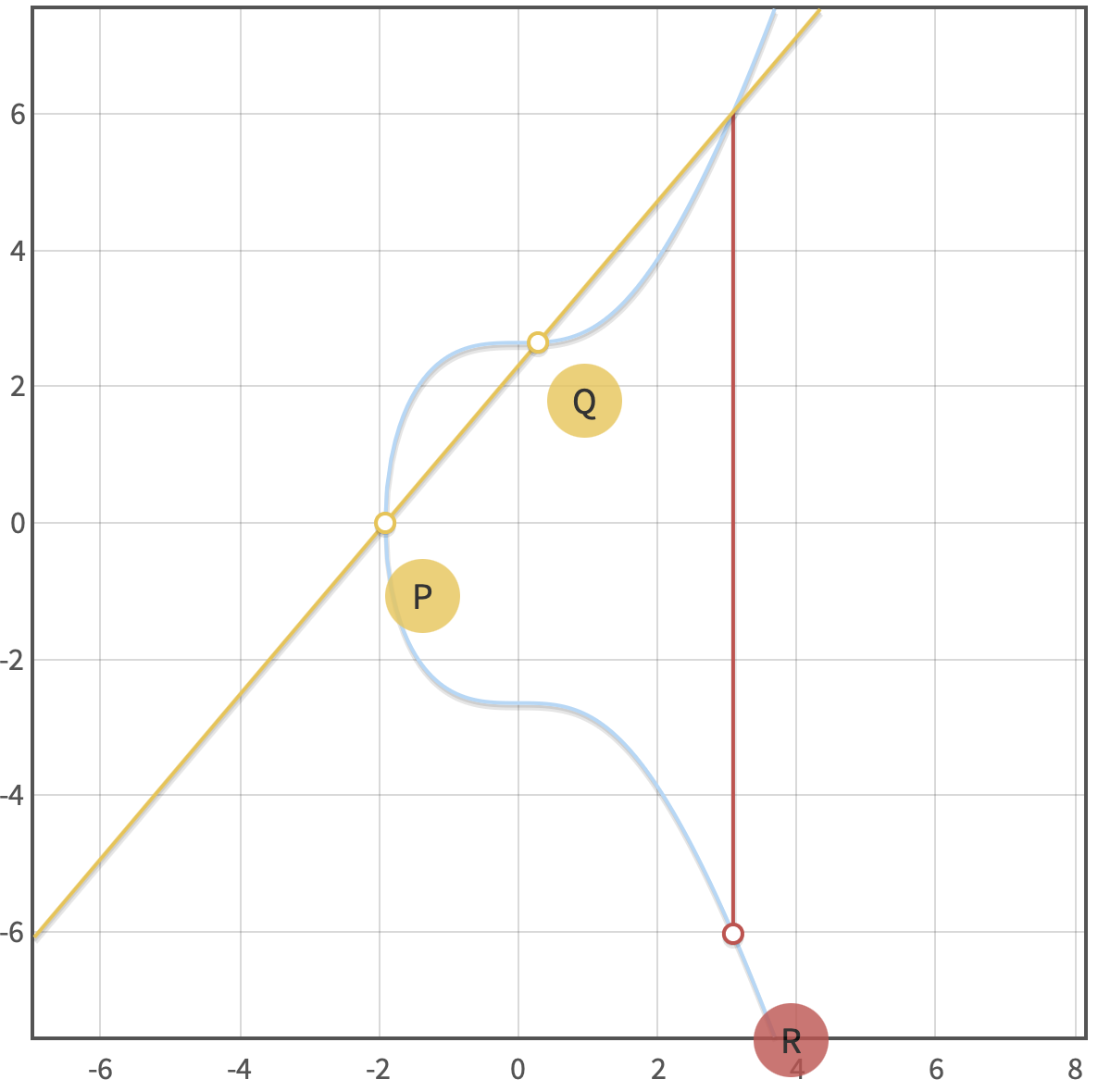
Curva adición Bitcoin
Este método geométrico funciona, pero necesita ser afinado. Particularmente necesitamos resolver las siguientes preguntas:
- ¿qué pasa si P=0 o Q=0?, debido a que hemos definido al 0 como el elemento de identidad, P+0=P y 0+Q=Q, para cualquier P y Q.
- ¿qué pasa si P=-Q?, en este caso la línea que pasa por P y Q es vertical y no intersecta un tercer punto. Pero si P es el inverso de Q, entonces tenemos que P+Q=P+(-P)=0 de la definición de inverso.
- ¿qué pasa si P=Q?, en este caso hay una infinidad de líneas pasando por el punto, pero la que nos interesa es la tangente al punto.
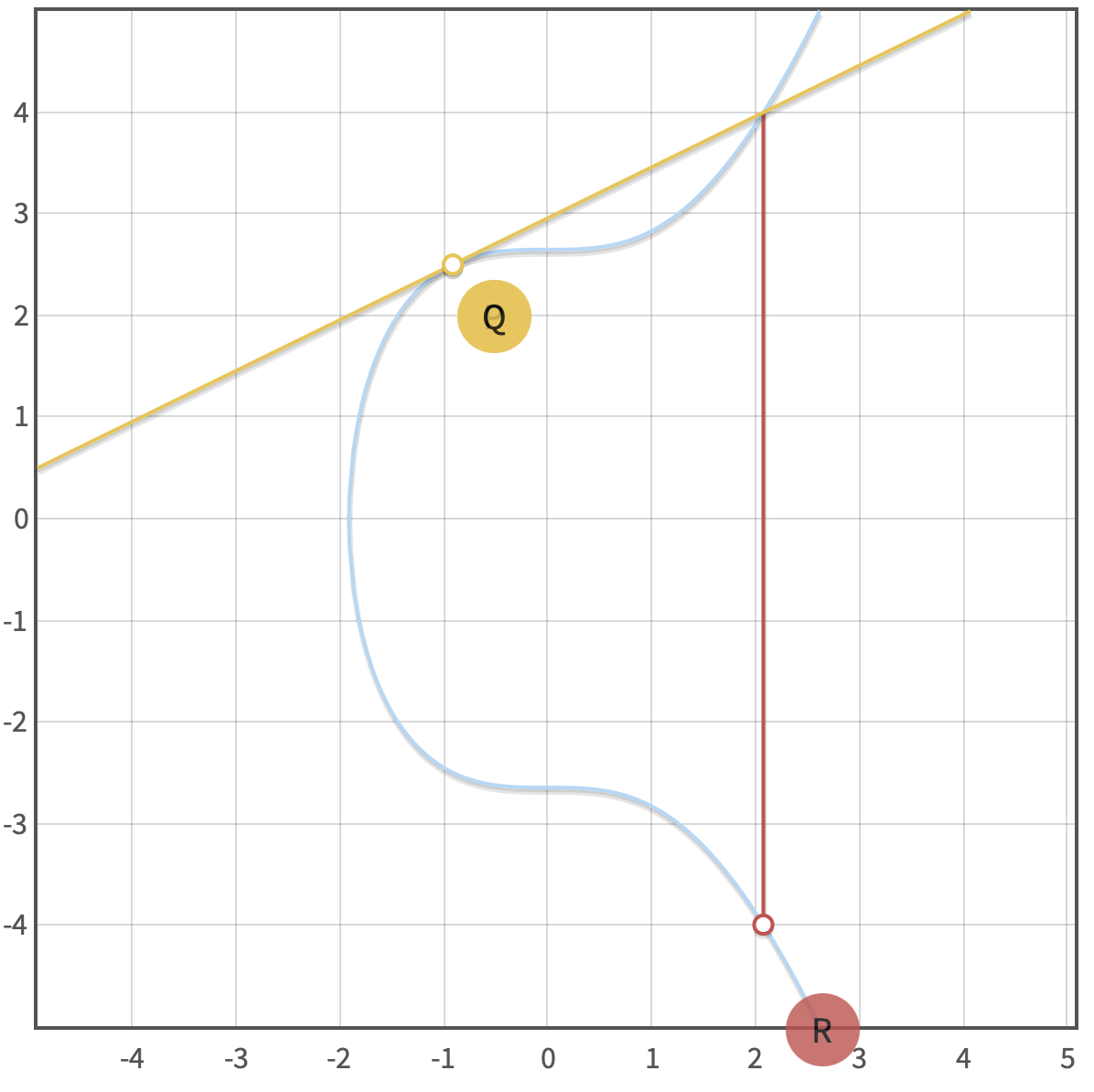
Curva tangente Bitcoin
Suma algebraica
Si queremos en algún momento construir un algoritmo para la adición de puntos debemos construir un método algebraico. Eliminemos por lo pronto los casos en los que P+(-P)=0 y en el que P+0=0+P=0 y concentrémonos en los dos casos que quedan: cuando P y Q son distintos y cuando P y Q son iguales.
Si P y Q son distintos, P1=(x1,y1), P2=(x2,y2), P3=(x3,y3), la línea que pasa por ellos tiene una pendiente, esta se calcula de la siguiente forma:
\[m = {yp - yq \over xp - xq} \]
podemos utilizar la pendiente para calcular x3 y una vez que obtengamos x3 podemos calcular y3. P3 puede obtenerse utilizando la siguientes formulas, que se obtienen después de hacer las sustituciones y despejar (no incluimos los cálculos en este post para mantener su tamaño dentro de lo razonable):
\[x3 = s^2-x1-x2 \]
\[y3 = s(x1-x3)-y1 \]
Si P y Q son iguales, P1=(x1,y1), P2=(x1,y1), P3=(x3,y3),en este caso debemos utilizar la tangente al punto, para calcular la pendiente m, recurrimos al cálculo para obtener la derivada de la ecuación de nuestra curva (no incluimos los cálculos en este post para mantener su tamaño dentro de lo razonable):
\[m = {3x1^2 + a \over 2y1} \]
Una vez que utilizamos la pendiente, hacemos las sustituciones y despejamos podemos obtener las formulas (no incluimos los cálculos en este post para mantener su tamaño dentro de lo razonable):
\[x3 = s2-2x1 \]
\[y3 = s(x1 - x3) - y1 \]
Hasta aquí nos hemos concentrado en las características principales de las curvas elípticas, la curva particular que utiliza Bitcoin, así como una perspectiva gráfica y otra algebraica de la adición de puntos, en un próximo post introduciremos el tema de los cuerpos finitos, su relación con las curvas elípticas y veremos como se deriva la llave pública a partir de una llave privada.
Criptografía Bitcoin, Curvas elípticas sobre cuerpos finitos
